Matlab中分层聚类

一般分层聚类分为以下几步：

分步聚类：（1）用pdist函数计算样本之间的距离，确定两两样本之间的距离或相似性（这个和选择的计算pdist的方法有关系）；（2）用linkage函数定义之间的连接；（3）用cophenet函数评价聚类效果；（4）用cluster函数进行聚类。

clusterdata 一个可完整实现聚类算法的函数，是以下pdist、linkage和cluster函数的综合。

pdist 计算样本点之间的距离，一般在计算距离之前用zscore函数对数据做标准化；

(另外，可以用squareform对pdist得到的距离用距离矩阵的形式呈现)

% Y = pdist(X);

linkage 以pdist的距离为输入，根据两两对象之间的距离进行聚类，输出为两两节点连接的顺序和他们之间的距离；

% Z = linkage(Y);

dendrogram 绘制linkage得到的聚类树，倒U型的高度代表对象间的距离

% dendrogram(Z);

cophenet 验证距离树的合理性，即对比cohpenetic距离与pdist函数计算的原始数据的距离之间的相关性，当然，相关值越接近于1说明聚类效果越好

% c = cophenet(Z, Y)

inconsistent 列出聚类树中各连接的不一致系数，这个值通过比较连接的高度和其下层连接的平均高度来计算，因此对于两个明显区别聚类的连接，其不一致系数较高。

% I = inconsistent(Z)

cluster 设定阈限（不一致性次数的阈值或最大cluster的个数），对原始数据进行聚类

% T = cluster(Z, ‘cutoff’, 1)

下面是一个例子：

采用猫的脑区连接信息。

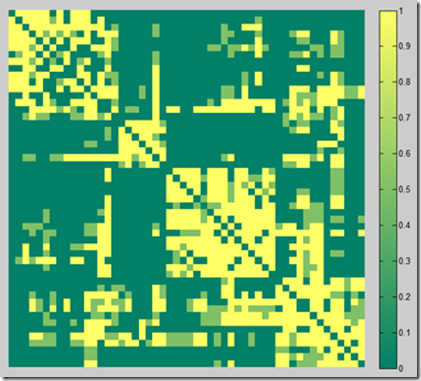
根据连接pattern对脑区进行聚类，代码如下：

catmatfile = ‘./toolbox/BCT/cat.mat’;
catmat = load(catmatfile);
X = (catmat.CIJctx’ + catmat.CIJctx)/2; % 只是为了把原始的连接矩阵搞成对称的
Y = pdist(X, ‘cityblock’);
Z = linkage(Y);
c = cophenet(Z, Y);
% c = 0.7254 in this analysis
dendrogram(Z, ‘LABELS’, catmat.Names);

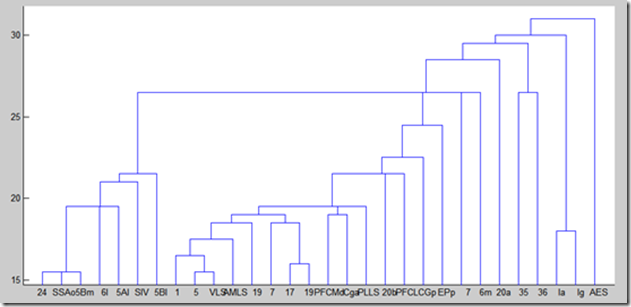
根据上面计算cophenetic系数为0.7254，结果不是很烂；

从聚类树上看，某些脑区可以根据其相似的连接pattern聚为相应的几类。